§03.4_非对称密码算法(Rsa 离散对数)【最且唯一难】
Categories:
少于1分钟
离散对数问题
- 有限域:DSA、ElGamal
- 椭圆曲线:ECDSA、SM2
加密表达式
通常遵循一些书写规则,以确保清晰和一致性:
- 变量命名:
- 使用简明且具有描述性的符号,例如 C表示密文,M表示明文,K表示密钥。可以加上下标以指明具体上下文,
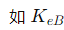 。
。
- 使用简明且具有描述性的符号,例如 C表示密文,M表示明文,K表示密钥。可以加上下标以指明具体上下文,
- 函数表示:
- 使用清晰的函数表示法 E,以表明这是一个加密操作。保持函数名称简短,便于理解。
- 括号使用:
- 函数参数使用括号明确区分,确保逻辑清晰。例如,
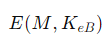 中,括号包围了所有输入。
中,括号包围了所有输入。
- 函数参数使用括号明确区分,确保逻辑清晰。例如,
- 一致性:
- 在整个文档或讨论中保持符号和术语的一致性,以避免混淆。
- 上下文说明:
- 在首次使用表达式时,最好提供简要说明,以帮助读者理解每个符号的含义。
遵循这些规则有助于确保表达式的可读性和可理解性,使得复杂的密码学概念更易于传达。
素数
不可被“分解”的数, 素数是大于1的自然数,且只能被1和它自身整除。换句话说,素数没有其他的因数。比如,2、3、5、7、11都是素数。最小的素数是2,它也是唯一的偶素数,其余的素数都是奇数。
欧拉函数


乘法逆元

2与二分之一互为倒数,乘积为1.


欧几里得算法与同余

求解乘法逆元


RSA计算
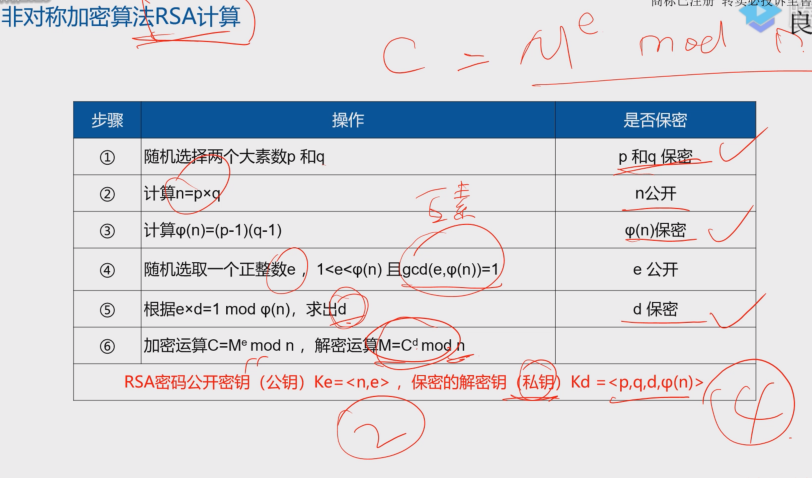
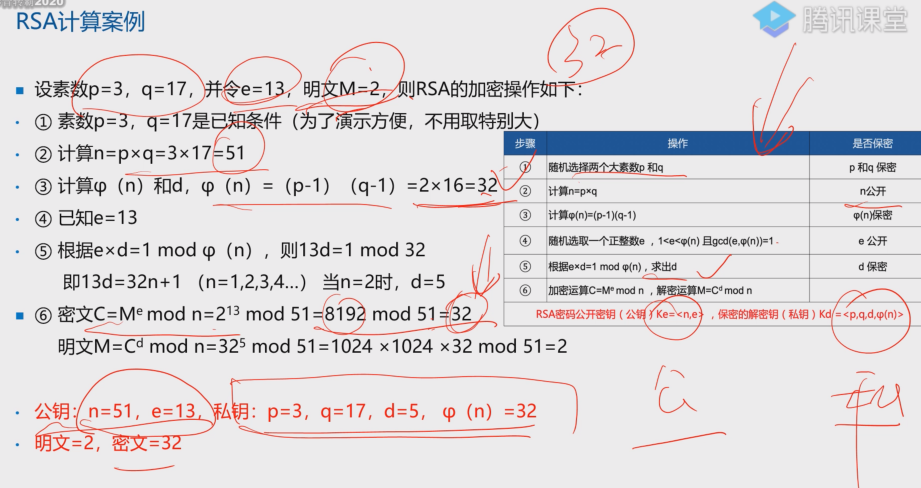

d为整数,n从1开始带入即可


私钥数字签名
公钥数据加密
RSA安全性
